こんにちは。マスムネです。今回の記事は,難問だけどクセになる良問シリーズの
記念すべき第1弾です!
このシリーズでは,難問の解法を学ぶことで,数学の応用力を高めることができるエッセンスを得ていくシリーズになります。まずは,中学数学3年間を網羅していこうと思っています。
よろしくお願いします!
では問題です。
問. 9991を素因数分解しなさい。
いや〜シンプルな問題ですね〜。私は、この問題の解き方も好きですが、難易度の割に問題文がシンプルすぎるところも好きです。
みなさんはどう進めていきますか?
では,解説していきます。
【解説】
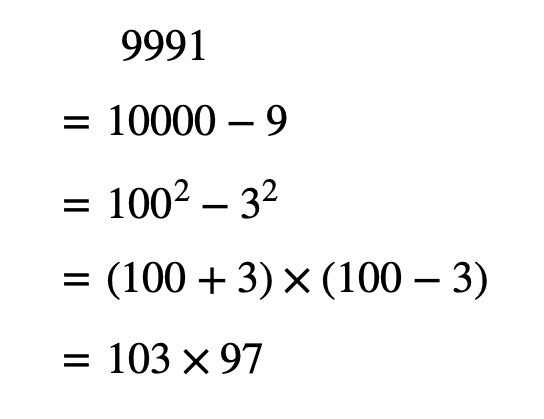
103と97はともに素数なので、これで素因数分解は完了している。
【答え】9991=103×97
解法としては、
①9991が因数分解できる数式に変換できることを見抜く。
② 下記のような和差の因数分解を利用する。
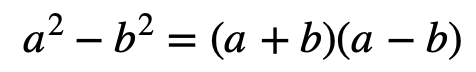
この2つがポイントである。
そして,この良問から得られる「他の問題に応用できるエッセンス」
略して【オーエス】は、
素因数分解するには、素数を探すだけでなく、因数分解を利用する視点も持っておくということ。
今回はこれにて終了です。
ではまた,いろいろな単元の難問かつ良問を紹介していきます。






コメント